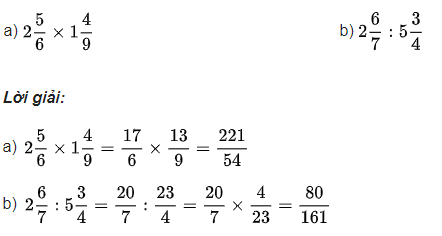Toán lớp 5 phép nhân, Phép nhân hỗn số lớp 5. Bài viết này giới thiệu đến các bạn nội dung lý thuyết và hướng dẫn làm bài tập giúp các em có kiến thức rộng trong quá trình làm các bài toán khó. Mời các bạn cùng tìm hiểu.
Lý thuyết về phép nhân Lớp 5
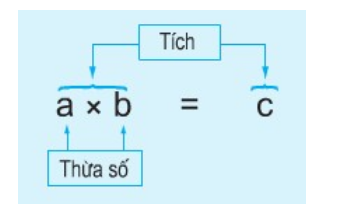
Phép nhân các số tự nhiên, phân số, số thập phân đều có các tính chất sau:
Tính chất giao hoán: a x b = b x a
Tính chất kết hợp: a x b x c = a x (b x c)
Nhân một tổng với một số: (a + b) x c = a x c + b x c
Phép nhân có thừa số bằng 1: 1 x a = a x 1 = a
Phép nhân có thừa số bằng 0: 0 x a = a x 0 = 0.
Tìm hiểu thêm :
Lý thuyết về phép nhân hỗ số
Định nghĩa hỗn số là gì?
Hỗn số là kết quả của việc viết gọn tổng của một số tự nhiên nguyên dương với một phân số dương bằng cách bỏ dấu cộng xen giữa chúng. Như vậy, một hỗn số gồm hai phần: phần nguyên và phần phân số.
Số đối của hỗn số này cũng được gọi là một hỗn số.
Hỗn số được viết dưới dạng 
. Phần phân số của hỗn số luôn luôn nhỏ hơn 1.
Cách đổi hỗn số thành phân số
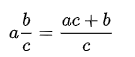
Đổi phân số hoặc hỗn số dương
Nếu phân số dương lớn hơn 1, ta có thể viết nó dưới dạng hỗn số bằng cách: chia tử cho mẫu. Thương tìm được là phần nguyên của hỗn số, phần phân số có tử là số dư là tử, còn mẫu vẫn là mẫu đã cho.
Nếu muốn đổi một hỗn số dương dưới dạng một phân số, thực hiện nhân phần số nguyên với mẫu rồi cộng với tử, kết quả tìm được là tử của phân số, còn mẫu vẫn là mẫu đã cho.
Đổi phân số hoặc hỗn số âm
Khi viết một phân số âm dưới dạng hỗn số, ta chỉ cần viết số đối của nó dưới dạng hỗn số rồi đặt dấu trước kết quả nhận được.
Tương tự như vậy, khi viết một hỗn số âm dưới dạng phân số, chỉ cần viết số đối của nó dưới dạng phân số rồi đặt dấu “-“ trước kết quả.
Cách nhân chia hỗn số
Phương pháp giải:
Khi nhân hoặc chia một hỗn số với một số nguyên, có thể viết hỗn số dưới dạng tổng của một số nguyên và một phân số.
Bài tập
Bài 1
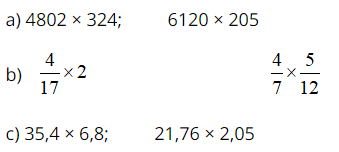
Lời giải
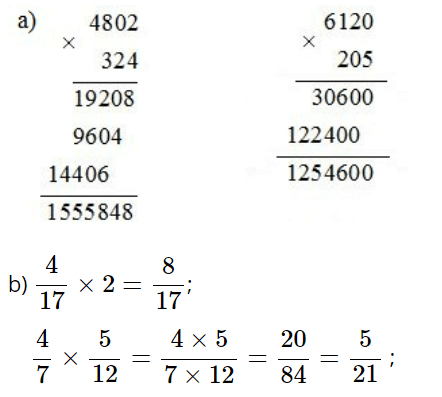
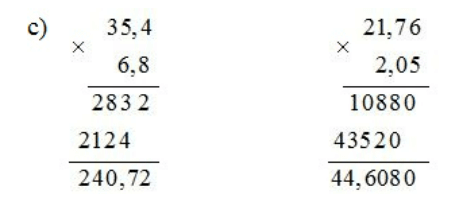
Bài 2 : Thực hiện phép tính
